Rovnica sveta

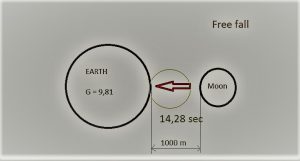
Predstavte si, že by teleso o hmotnosti mesiaca padalo voľným pádom na zem so štartom tohto pádu z výšky tisíc metrov.

Podľa gravitačného zákona je zrýchlenie telesa pri voľnom páde nezávislé od hmotnosti tohto telesa :

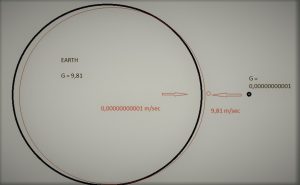
podľa tejto časti gravitačného zákona je teda zrýchlenie každého telesa pri voľnom páde 9,81 metra za sekundu, čo zodpovedá gravitačnej sile našej planéty,  ktorá touto silou svojej príťažlivosti priťahuje takéto teleso k sebe.

To, akú rýchlosť dosiahne teleso vo voľnom páde pri dopade z výšky tisíc metrov podľa tejto časti gravitačného zákona, kde sa tvrdí, že zrýchlenie telesa vo voľnom páde je nezávislé od jeho hmotnosti vypočítame takto:

pričom v je dosiahnutá rýchlosť,  g je zrýchlenie, ktoré je pri voľnom páde  9,81 metrov za sekundu, teda zodpovedá gravitačnej sile planéty Zem a s je prekonaná vzdialenosť

140 m/s je teda rýchlosť ktorú dosiahne teleso vo voľnom páde z výšky tisíc metrov pri dopade na povrch planéty

vydelením tohto výsledku dvomi zistíme priemernú rýchlosť tohto telesa pri voľnom páde, teda 140 : 2 = 70 m/s.  Ak vydelíme dĺžku voľného pádu priemernou rýchlosťou, teda 1000 : 70 zistíme čas trvania tohto voľného pádu teda 14,28 sekúnd.

Lenže tento istý zákon tvrdí, že:

dve telesá svojou gravitačnou silou pôsobia na seba navzájom a teda sa navzájom priťahujú.

To znamená, že nie len Zem priťahuje k sebe vďaka svojej gravitačnej sile telesá, ale aj každé teleso pôsobí svojou vlastnou gravitáciou na planétu zem a priťahuje ju k sebe.

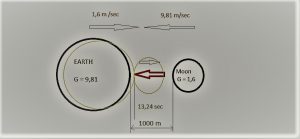
Teleso o hmotnosti mesiaca vytvára vďaka svojej mase gravitačnú silu G= 1,6. Takže podľa tejto časti gravitačného zákona priťahuje toto teleso planétu Zem k sebe a tento pohyb našej planéty k takémuto telesu má zrýchlenie rovnajúce sa gravitačnej sile tohto telesa teda 1, 6 m/s

Takže až keď dosadíme do tejto rovnice aj gravitačnú silu telesa vo voľnom páde, teda budeme počítať podľa tej časti gravitačného zákona, kde sa tvrdí, že dve telesá sa navzájom svojou gravitačnou silou priťahujú, zistíme reálny výsledok trvania tohto voľného pádu.

Takže rovnica pre tento výpočet by mala vyzerať potom takto:

pričom g1 je gravitačná sila planéty teda G = 9,81 a g2 je gravitačná sila telesa ktoré sa nachádza vo voľnom páde, pretože ako sme si už ukázali na znení zákona,  pôsobia dve telesá na seba navzájom a teda musíme tieto gravitačné sily oboch telies  spočítať, aby sme zistili,  aké bude skutočné zrýchlenie pri takomto voľnom páde.

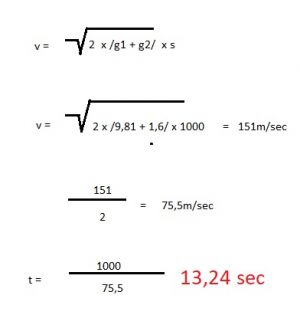
Takže v našom prípade, keďže teleso o hmotnosti mesiaca vytvára gravitačnú silu G= 1,6 musí tento prepočet vyzerať takto:

v = druhá odmocnina z 2 x  / 9,81 + 1,6/  x 1000

výsledok 151 m/s predstavuje vzájomnú rýchlosť telesa o hmotnosti mesiaca a našej planéty v momente ich nárazu na seba, teda pri dopade tohto telesa na povrch planéty.

Z toho teda vyplýva, že priemerná rýchlosť by bola 151 : 2 = 75, 5 m/s a takýto voľný pád z výšky tisíc metrov byť teda trval 1000 : 75, 5 = 13, 24 sekúnd a nie 14, 28 sekúnd, ako to tvrdí gravitačný zákon vo svojej časti o tom, že rýchlosť telesa pri voľnom páde je nezávislá od hmotnosti takéhoto telesa, pretože gravitačná sila je priamo úmerná hmotnosti telesa.

Z tohto príkladu by malo byť každému jasné, že tvrdenie v gravitačnom zákone o tom, že rýchlosť, alebo zrýchlenie telesa pri voľnom páde je nezávislá od jeho hmotnosti odporuje akejkoľvek logike a aj tvrdeniu o vzájomnom pôsobení gravitačných síl dvoch telies.

Pretože aj pri voľnom páde ktorý je výsledkom pôsobenia gravitácie, pôsobí planéta Zem na padajúce teleso a padajúce teleso pôsobí silou svojej gravitácie na planétu zem a táto Gravitácia je závislá od hmotnosti tohto telesa.

Pri menších telesách je účinok gravitácie týchto telies na planétu zem taký nepatrný, že ho nevieme pri experimentoch namerať  pozorovaním rozdielne ťažkých telies vo voľnom páde. Veď aj matematicky sa tento účinok teda rozdiel ukáže až niekde ďaleko za desatinnou čiarkou vo výpočte:

To ale ešte stále neznamená, že tieto nepatrné účinky gravitácie takýchto menších telies môžeme jednoducho ignorovať, pretože ak sa fyzika považuje za exaktnú vedu, potom v nej takéto nezmyselné tvrdenie, teda že zrýchlenie telesa pri voľnom páde je nezávislé od hmotnosti tohto telesa nemajú čo hľadať.

Tu je link na moje video s podrobnosťami k tejto téme:

https://www.youtube.com/watch?v=BPSq9t1dWkw&t=2s

Pavol Nemeš